four in a row, min max 알고리즘, Alpha beta pruning 에 대하여

안녕하십니까. 제 개인 컴퓨터에 있는 자료를 정리하다 보니, 학부 3학년때 제출 하였던 인공지능 과제를 찾게 되어서 블로그 포스팅 합니다. 

코드 링크 : https://github.com/Myeongjoon/examples/blob/master/artificial%20intelligence/four_in_a_row.html

(사실 코드는 대부분 짜지 않았다는 점..)

해당 인공지능 수업을 할 당시는 구글에서 알파고를 발표하였던 그시기였기 때문에 인공지능 수업이 핫하였고, 그중 게임 이론이 중심이었습니다. 인공지능에서 쉽게 다룰 수 있는 내용이 트리 구조를 통한 게임 인공지능 알고리즘이었고 자연스럽게 텀 프로젝트는 four-in-a-row를 통한 리포트가 되었습니다. 

Four In A Row

four in a row 라는 게임은 간단한 게임입니다. 

테트리스 처럼 위에서 아래로 돌이 떨어지는 게임이고, 상대방과 내가 번갈아서 한번씩 돌을 사용 합니다.

위로 4줄, 옆으로 4줄, 대각선으로 4줄 어떤식이든 4개로 이루어진 줄을 하나를 만들면 게임에서 이기게 됩니다.

위의 사진에서 보면 파란색 돌 기준으로 대각선 하나가 4개의 돌로 되어 있고, 따라서 파란색 돌의 승리 입니다.

Min Max 알고리즘

위의 게임의 인공지능을 구현하는데에 있어서 여러 방법이 있겠지만 수업시간에서는 민맥스 알고리즘을 중심으로 진행하였습니다.  

민맥스 알고리즘은 최대 n번째 이후까지의 수를 예측을 합니다. 이는 두 플레이어가 최선의 수를 두는 것을 가정을 하며, 결국 누군가가 이기려면 그사람은 이길 경우가 가장 높은 수를 두고, 반대로 상대의 수를 예측을 하면 상대가 이길 경우가 가장 낮은 수를 예측을 해야합니다.

아래 사진은 Geekforgeeks라는 사이트에서 가져왔습니다.

아래는 3개의 수까지 예측을 하는 경우 이며, 마지막 노드의 숫자들은 해당 경우의 수에서의 점수 입니다. 점수를 매기고 난 후에는 차례로 내차례에는 최대한 이길 숫자가 높은 경우로, 상대 차례에는 상대도 이기는 수를 생각할 테니 가장 상대의 점수가 낮은 수를 선택 합니다. 

Alpha-Beta Pruning

프루닝이라는 단어는 가지 치기를 말합니다. 주어진 민맥스 알고리즘을 좀더 속도가 빠르게 최적화 시켜주는 알고리즘입니다. 

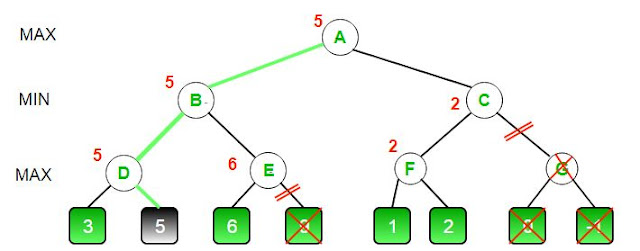
alpha라는 변수는 max phase에서 정해지는 값이고, beta라는 변수는 min phase에서 정해지는 변수 입니다.

위의 예시에서 D의 경우를 보면 최댓값은 5이고, B 입장에서는 D를 통해서 적어도 5라는 수를 확보 했다고 볼 수 있습니다. E를 보는데에 있어서 5보다 크다고 하면 굳이 볼필요가 없게 됩니다. 따라서 E는 왼쪽 노드가 6이라는 것을 알았고, E는 max phase이며 더이상 낮아질 수 없는 상황 입니다. 따라서 굳이 E 오른쪽 아래를 볼 필요는 없으므로 계산하지 않습니다.

위의 예시에서는 겨우 하나의 노드로 보이지만 3번째 노드의 결과값들이 각각 depth 4,5,6,... 등의 결과값을 통해서 얻었다면 이때 연산은 많이 줄일 수 있습니다. 

코드로 보자

해당 과제는 min-max 알고리즘을 통하여 리포트를 작성하는 과제였습니다. 과제에서는 외부 사이트를 참조하여도 무방하다고 하였고, 당시에는 6전공을 수강하기도 하고, 굳이 처음부터 개발할 필요는 없다고 판단하여 외부 사이트를 참조하였습니다. 

코드의 내용은 주석에 첨부하였습니다.

function MaxMove (player, level, ParentMin, want) {
//level은 depth를 뜻함. 
//ParentMin은 베타값을 의미한다. 위의 E 노드 입장에서는 5를 받게 된다.
//want는 맨 상위 노드에서는 다음에 두어야 할 정보가 필요하며, 하위 노드들은 아랫 노드의 
//점수만 필요하기 때문에 구분하였다.
    if (level <=0) {  // 0보다 작으면 내가 보려한 수는 다 본것이다.
        return GetBoardVal(player);
    } else {
    
        var MaxCol = 0;
        var MaxVal = -WINVAL*10;
        //돌을 넣을 수 있는 7가지 경우의 수에 대하여
        for(var col = 0; col<COLS; col++) {
            //freerow 부분은 해당 row가 돌을 놀수 있는 상태인지를 체크 합니다.
            var row = freerow(col);
            if (row>=0) {

                board[row][col] = player;
                //해당 경우를 두었다고 가정을 하고 한 depth 내려 갑니다. 
                var TheVal = MinMove(player, level-1, MaxVal, "Val");
                board[row][col]=0; // undo move
                
                if (TheVal == WINVAL) return WINVAL; // game won 
                //이부분이 걸리게 되면 알파 베타 프루닝이 작용 합니다. 
                //위의 B-E 노드 경우 입니다.
                if(TheVal > ParentMin) {
                    return TheVal;
                } else {
                    if (TheVal > MaxVal ) {
                        MaxVal = TheVal ;
                        MaxCol = col;
                    }
                }
            }
        }
        if (want=="Val") {
            return MaxVal;
        } else {
            return MaxCol;
        }
    }
}

function MinMove (player, level, ParentMax, want) {

    if (level <=0) { // NB or game ended
        return GetBoardVal(player);
    } else {
    
        var MinCol = 0;
        var MinVal = WINVAL*10;
        
        for(var col = 0; col<COLS; col++) {
        
            var row = freerow(col);
            if (row>=0) {
        
                if (player==RedNum) { // do move with OPPOSITE player
                    board[row][col] = BlkNum;
                } else {
                    board[row][col] = RedNum;
                }
        
                var TheVal = MaxMove(player, level-1, MinVal, "Val");
                board[row][col]=0; // undo move
                
                if (TheVal == -WINVAL) return -WINVAL; // game won by opponent
                
                
                if(TheVal < ParentMax) {// no need to go further, because the min will be less than the max already found
                    return TheVal;
                } else {
                    if (TheVal < MinVal ) {  // less than
                        MinVal = TheVal;
                        MinCol = col;
                    }
                }
            }
        }
        return MinVal;
    }
}

function GetBoardVal(player) {
    //이기지 못한 경우를 대비하여 점수를 결정하는 함수.

    //각 돌에 대하여 가능한 row의 돌의 경우의 수에 대하여 점수를 매긴다. 내돌이 많이 이어져 있으면 높은 점수이고,

    //상대방이 많으면 낮은 점수이다. 

    //휴리스틱 함수는 각자 구현하는 방식에 따라 다를 수 있다.

    thesum = 0;
    
    for(var rowno=0; rowno<linecount; rowno++) {
        var theline = linecoords[rowno];
        thesum += Strength(player,theline[0],theline[1],theline[2],theline[3]) * theline[4];
    }

    return thesum;
}

코드 수정 부분

위의 코드는 사실 제가 짜진 않았고, 사이트에 있는 코드 입니다. 

제가 추가한 부분은 첫 3수 정도는 하드 코딩을 하였습니다. 그 이유는 첫수에서는 절대로 승리하는 수를 볼 수 없기 때문에 로직이 작동하지 않습니다. 물론 10수까지 본다고 가정하면 극한의 경우 1자로 세우는 경우가 있을 수 있으나, 일반적인 데스크탑으로는 10수 이상으로 갈시 1분내에 연산이 되지 않습니다. 저도 또한 9수까지는 1분내에 되었기 때문에 9수까지만 사용하였습니다. 

휴리스틱을 통해서 생각을 할시 보통 가운데에 넣으면 이긴다는 것을 논문에서도 볼 수 있었습니다.

한계

민맥스 알고리즘의 한계는 명확 합니다.

서로 최선의 수를 둔다고 가정을 하고 프루닝을 하기 때문에 상대방이 다른 수를 통해서 최적의 수를 찾아내었다고 하면 예측은 전혀 의미가 없어지게 됩니다. 

또한 프루닝을 하였다고 하지만 사실이는 명확히 안봐도 되는 수라고 할수 있는데 그렇게 보면 결국 모든 경우의 수를 직접 따져야 합니다.