Factorization machines 리뷰
논문 링크 : https://www.csie.ntu.edu.tw/~b97053/paper/Rendle2010FM.pdf
III. FACTORIZATION MACHINES (FM)

A. SVM model
B. Parameter Estimation Under Sparsity
C. Summary
A. Matrix and Tensor Factorization
B. SVD++
C. PITF for Tag Recommendation
D. Factorized Personalized Markov Chains (FPMC)
E. Summary
Abstract
이 논문에서는 SVM과 Factorization Model의 장점을 결합한 새로운 모델을 다룬다.
두개의 모델 모두 feature vector를 다루지만 FM은 factorized 파라미터를 사용하고 이를 통해서 sparse한 데이터를 SVM 보다 더욱 잘 다룬다고 한다.
FM은 SVM에 비하여 선형 시간을 가진다고 한다.
일반적인 MF 모델은 general한 인풋에는 적절하지 않아서 이를 해결하려고 한다.
SVM은 prediction을 하려면 데이터가 어느정도 저장이 되어야 하지만 MF는 factorization 함.
두개의 모델 모두 feature vector를 다루지만 FM은 factorized 파라미터를 사용하고 이를 통해서 sparse한 데이터를 SVM 보다 더욱 잘 다룬다고 한다.
FM은 SVM에 비하여 선형 시간을 가진다고 한다.
일반적인 MF 모델은 general한 인풋에는 적절하지 않아서 이를 해결하려고 한다.
SVM은 prediction을 하려면 데이터가 어느정도 저장이 되어야 하지만 MF는 factorization 함.
I. INTRODUCTION
SVM이 sparse하고 convex(비선형)한 kernel space에서는 효과적이지 않음을 다루려고 한다. FM 모델은 일반적인 데이터에는 적용하기 어렵다. 이 둘의 장점을 결합한 Factorization Machine을 소개한다. 또한 이는 선형적으로 계산이 가능하며 선형적인 파라미터가 필요 하다.
In total, the advantages of our proposed FM are:
In total, the advantages of our proposed FM are:
- FMs allow parameter estimation under very sparse data where SVMs fail.
- FMs have linear complexity, can be optimized in the primal and do not rely on support vectors like SVMs. We show that FMs scale to large datasets like Netflix with 100 millions of training instances.
- FMs are a general predictor that can work with any real valued feature vector. In contrast to this, other state-ofthe-art factorization models work only on very restricted input data. We will show that just by defining the feature vectors of the input data, FMs can mimic state-of-the-art models like biased MF, SVD++, PITF or FPMC.
II. PREDICTION UNDER SPARSITY
Example 1
아래와 같은 영화 데이터를 가정
S는 유저 U의 영화 I에 대한 평점으로 볼 수 있음
 |
| Fig 1 |
III. FACTORIZATION MACHINES (FM)
A. Factorization Machine Model
1) Model Equation
degree d = 2일때 수식을 아래와 같이 정의 한다.
아래는 파라미터 space
아래는 dot product를 정의 한다.

A row vi within V describes the i-th variable with k factors. k ∈ N + 0 is a hyperparameter that defines the dimensionality of the factorization.
A 2-way FM (degree d = 2) captures all single and pairwise interactions between variables:
• w0 is the global bias.
• wi models the strength of the i-th variable.
• wˆi,j := hvi , vj i models the interaction between the ith and j-th variable. Instead of using an own model parameter wi,j ∈ R for each interaction, the FM models the interaction by factorizing it. We will see later on, that this is the key point which allows high quality parameter estimates of higher-order interactions (d ≥ 2) under sparsity.
2) Expressiveness
3) Parameter Estimation Under Sparsity
4) Computation
3) Parameter Estimation Under Sparsity
4) Computation
B. Factorization Machines as Predictors
FM은 여러 문제에 사용할 수 있음.
- Regression: yˆ(x) can be used directly as the predictor and the optimization criterion is e.g. the minimal least square error on D
- Binary classification: the sign of yˆ(x) is used and the parameters are optimized for hinge loss or logit loss.
- Ranking: the vectors x are ordered by the score of yˆ(x) and optimization is done over pairs of instance vectors (x (a) , x (b) ) ∈ D with a pairwise classification loss (e.g. like in [5]). In all these cases, regularization terms like L2 are usually added to the optimization objective to prevent overfitting.
C. Learning Factorization Machines
D. d-way Factorization Machine
2-way FM을 아래와 같이 d-way로 일반화 가능
 |
| d way FM |
i번째 파라미터는 PARAFAC 모델을 통하여 factorize 가능. 파라미터는 아래와 같음.
시간복잡도는 아래와 같지만 3.1에서 선형 가능함을 보였음.
E. Summary
FM은 전체 파라미터를 사용하지 않고 Factorization 하여 아래와 같은 이점을 가진다.
- The interactions between values can be estimated even under high sparsity. Especially, it is possible to generalize to unobserved interactions.
- The number of parameters as well as the time for prediction and learning is linear. This makes direct optimization using SGD feasible and allows optimizing against a variety of loss functions.
IV. FMS VS. SVMS
ㅇㅇA. SVM model
B. Parameter Estimation Under Sparsity
C. Summary
V. FMS VS. OTHER FACTORIZATION MODELS
ㅇㅇA. Matrix and Tensor Factorization
B. SVD++
C. PITF for Tag Recommendation
D. Factorized Personalized Markov Chains (FPMC)
E. Summary




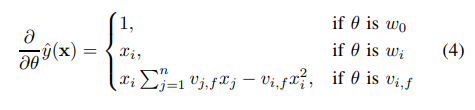




댓글
댓글 쓰기